What is Data Structure?
In interviews, proficiency in data structures is crucial for software engineering roles. Candidates are often tested on their understanding and application of fundamental structures like arrays, linked lists, trees, and graphs. The ability to choose and implement the appropriate data structure efficiently is essential for solving algorithmic problems and optimizing code. A solid grasp of these concepts not only showcases a candidate's technical expertise but also demonstrates their problem-solving skills in various scenarios.
What are different categories on Data Structure
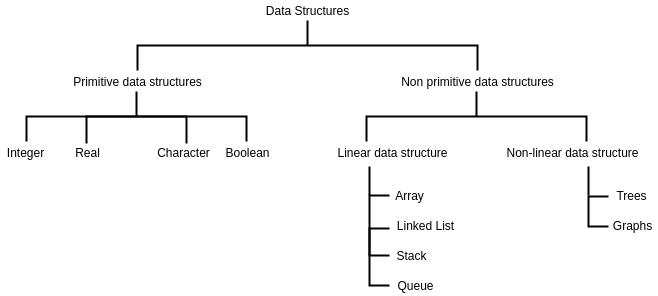
Primitive Data Types
Basic data types like integers, floating-point numbers, characters, and booleans.
Linear Data Structures
- Arrays: Contiguous memory storage for elements.
- Linked Lists: Elements linked through pointers.
- Stacks: Last In, First Out (LIFO) structures.
- Queues: First In, First Out (FIFO) structures.
- Heaps: Specialized trees used in priority queue implementations.
- Hash Tables: Key-value pairs with a hash function for efficient data retrieval.
Non-linear Data Structures
- Trees: Hierarchical structures with nodes connected by edges.
- Graphs: Collections of nodes connected by edges; can be directed or undirected.
- Trie: Tree-like structure for efficient retrieval of key-value data.
Understanding these categories and their implementations is crucial for effective problem-solving in coding interviews and real-world software development.
Time and Space Complexity
Time Complexity
Time complexity is a measure of the amount of time an algorithm takes to complete as a function of the size of the input. It's expressed using big O notation, which describes the upper bound of an algorithm's running time.
Examples in Python
-
Constant Time (O(1)):
my_list = [1, 2, 3, 4, 5] print(my_list[0]) # O(1) -
Linear Time (O(n)):
def linear_search(my_list, target): for item in my_list: if item == target: return True return False -
Quadratic Time (O(n^2)):
def bubble_sort(my_list): n = len(my_list) for i in range(n): for j in range(0, n - i - 1): if my_list[j] > my_list[j + 1]: my_list[j], my_list[j + 1] = my_list[j + 1], my_list[j]
Space Complexity
Space complexity is a measure of the amount of memory an algorithm uses as a function of the size of the input. It's expressed using big O notation.
Examples in Python
-
Constant Space (O(1)):
def constant_space_example(): a = 5 b = 10 result = a + b -
Linear Space (O(n)):
def linear_space_example(n): my_list = [0] * n for i in range(n): my_list[i] = i -
Quadratic Space (O(n^2)):
def quadratic_space_example(n): matrix = [[0] * n for _ in range(n)]
Understanding time and space complexity helps in analyzing and optimizing algorithms to ensure efficiency for different input sizes.
Different types of Complexities.
| Complexity | Type | Performance | Example |
|---|---|---|---|
| Time Complexity | Constant Time (O(1)) | Excellent, independent of input size | Accessing an element in an array |
| Linear Time (O(n)) | Moderate, linearly proportional to input size | Searching an element in a list | |
| Quadratic Time (O(n^2)) | Poor, proportional to the square of input size | Simple nested loop algorithms | |
| Logarithmic Time (O(log n)) | Good, particularly for large datasets | Binary search algorithm | |
| Exponential Time (O(2^n)) | Very poor, grows rapidly with input size | Recursive algorithms with branching |
| Complexity | Type | Performance | Example |
|---|---|---|---|
| Space Complexity | Constant Space (O(1)) | Excellent, fixed amount of memory used | Variables, simple calculations |
| Linear Space (O(n)) | Moderate, memory usage linearly proportional to input size | Arrays, lists | |
| Quadratic Space (O(n^2)) | Poor, memory usage proportional to the square of input size | 2D arrays, nested data structures | |
| Logarithmic Space (O(log n)) | Good, particularly for recursive algorithms | Binary search trees, recursive algorithms | |
| Exponential Space (O(2^n)) | Very poor, grows rapidly with input size | Recursive algorithms with exponential growth |
what are Basic operation on data structures?
Basic operations on data structures are fundamental actions that can be performed to manipulate and manage the data stored within these structures. The specific operations vary depending on the type of data structure. Here are some common basic operations for different types of data structures:
| Data Structure | Operation | Description |
|---|---|---|
| Arrays | Access | Retrieve or modify the value at a specific index. |
| Insertion | Add an element to the array (beginning, end, or index). | |
| Deletion | Remove an element from the array (beginning, end, index). | |
| Search | Find the index of a specific element in the array. | |
| Linked Lists | Insertion | Add a new node to the linked list (beginning, end, after). |
| Deletion | Remove a node from the linked list (beginning, end, index). | |
| Traversal | Visit each node in the linked list. | |
| Stacks | Push | Add an element to the top of the stack. |
| Pop | Remove the element from the top of the stack. | |
| Peek/Top | View the element at the top without removing it. | |
| Queues | Enqueue | Add an element to the rear/end of the queue. |
| Dequeue | Remove the element from the front of the queue. | |
| Front/Rear | Retrieve the element at the front or rear without removal. | |
| Trees | Insertion | Add a new node to the tree. |
| Deletion | Remove a node from the tree. | |
| Traversal | Visit nodes in a specific order (in-order, pre-order, etc.). | |
| Hash Tables | Insertion | Add a key-value pair to the hash table. |
| Deletion | Remove a key-value pair from the hash table. | |
| Search | Look up the value associated with a given key. | |
| Graphs | Add Vertex | Add a new vertex to the graph. |
| Add Edge | Add a new edge between two vertices. | |
| Remove Vertex/Edge | Delete a vertex or an edge from the graph. | |
| Traversal | Visit vertices and edges in the graph (depth-first, breadth-first). |